|
城區(qū)35kV電纜線路末端最優(yōu)無功補(bǔ)償容量研究
張宇澤1, 卓建宗2, 董洋1, 王建1
1.國網(wǎng)天津市電力公司城西供電分公司,天津300190; 2.國網(wǎng)福建省電力有限公司福州供電公司,福州350004)
摘要:利用潮流計算推導(dǎo)城區(qū)35kV電纜線路線損的數(shù)學(xué)公式,建立了以線損最低為目標(biāo)的城區(qū)35kV電纜線路末端最優(yōu)無功補(bǔ)償容量的數(shù)學(xué)模型。利用 PSASP仿真計算驗證了該模型的正確性,并給出了4種常見型號35kV電纜線路在不同負(fù)載率下的末端最優(yōu)無功補(bǔ)償容量數(shù)值,為城區(qū)供電企業(yè)降損提供參考 。
關(guān)鍵詞:電纜線路;線損;最優(yōu)無功補(bǔ)償
0 引言
為節(jié)約土地資源,市容美觀,我國城區(qū)35kV配電網(wǎng)逐漸采用電纜線路取代架空線路 。電纜線路具有故障率低 ,供電可靠性高 ,對周圍環(huán)境影響小等優(yōu)勢 ,但其對地電容是架空線路的幾十倍 ,充電功率比相同電壓等級、相同長度的架空線路大得多 ,存在輕負(fù)荷時電纜線路向上級電源倒送無功的問題 ,增大電網(wǎng)網(wǎng)損 ,影響供電經(jīng)濟(jì)性 。針對電纜線路及含電纜線路電網(wǎng)的無功補(bǔ)償問題 ,諸多學(xué)者進(jìn)行了一系列研究 。文獻(xiàn)分析了全電纜高壓 (110kV)配電網(wǎng)的無功電壓特性 ,提出一種基于電纜網(wǎng)無功潮流特性的高壓配電網(wǎng)無功補(bǔ)償方法 ,對電纜網(wǎng)電源側(cè)變電站和負(fù)荷側(cè)變電站無功補(bǔ)償協(xié)同控制 ,改善高壓配電網(wǎng)電壓質(zhì)量 。文獻(xiàn)利用潮流計算 ,得到了兩種長度 YJV22-3x240型 10kV電纜線路在不同負(fù)載率下充電功率和消耗無功功率的數(shù)值 ,其研究結(jié)論是 4km長度的電纜線路在負(fù)載率低于 5%時存在向上級電網(wǎng)倒送無功的現(xiàn)象需要采用感性無功補(bǔ)償設(shè)備進(jìn)行無功調(diào)節(jié)。文獻(xiàn)分析了溫州電網(wǎng)小負(fù)荷方式下 110kV及以下電纜線路充電功率對電網(wǎng)無功平衡的影響 ,得到的結(jié)論是 ,變電站工程規(guī)劃設(shè)計中應(yīng)以小負(fù)荷方式下的潮流數(shù)據(jù)為依據(jù)確定感性無功補(bǔ)償裝置容量 。電纜出線較多的 220kV變電站應(yīng)配置電抗器 ,電纜率較高的 110kV變電站也應(yīng)考慮增設(shè)電抗器或靜止無功補(bǔ)償器 ( static var ompensator,SVC)就地補(bǔ)償電纜線路的充電功率 ,以改善 220kV及以下變電站在小負(fù)荷方式下的功率因數(shù) 。上述文獻(xiàn)從電壓 、無功潮流、功率因數(shù)等各方面論述了含電纜線路電網(wǎng)加裝感性無功補(bǔ)償裝置的必要性 ,但均未給出電纜線路最優(yōu)無功補(bǔ)償容量的計算方案 。
本文首先利用潮流計算推導(dǎo)出了城區(qū)35kV電纜線路線損的數(shù)學(xué)公式 ,建立了以線損最低為目標(biāo)的城區(qū) 35kV電纜線路末端最優(yōu)無功補(bǔ)償容量的數(shù)學(xué)模型;然后利用 PSASP仿真計算驗證了該模型的正確性 ,并給出了 4種常見型號 35kV電纜線路在不同負(fù)載率下的末端最優(yōu)無功補(bǔ)償容量數(shù)值 ,為城區(qū)供電企業(yè)降損提供參考 。
1 城區(qū)35kV電纜線路線損計算
利用潮流計算,推導(dǎo)城區(qū)35kV電纜線路線損的數(shù)學(xué)公式。由于城區(qū)35kV電纜線路的長度大多為2-5km,一般不會超過10km,且本文研究的問題無需計及線路的分布參數(shù)特性,故潮流計算中電纜線路用集中參數(shù)的∏型等值電路表示,計算參數(shù)包括電阻R 、電抗 X和電納 B 。電阻 R表征導(dǎo)體通過電流時產(chǎn)生有功功率損耗的效應(yīng);電抗 X表征線路流過交流電流時導(dǎo)線周圍產(chǎn)生磁場效應(yīng) ,感應(yīng)電動勢阻礙電流流過的能力 ;電納 B表征帶電導(dǎo)線周圍的電場效應(yīng) 。電纜線路三相導(dǎo)體間的距離遠(yuǎn)小于相同電壓等級的架空線路 ,故其電抗 X比相同長度的架空線路小得多 ,而電納 B遠(yuǎn)大于具有相同截面積的架空線路 。電纜線路導(dǎo)體的截面可能不是規(guī)則的圓形 ,導(dǎo)體周圍的介質(zhì)不是空氣,外包還有鋁 (鉛 )包和鋼鎧 ,故其參數(shù)很難用數(shù)學(xué)方法求得 ,一般由制造廠商事先測得并在產(chǎn)品說明書中提供 。幾種常見 35kV電纜的電氣參數(shù)見表 1 。
表1幾種常見35kV電纜電氣參數(shù)
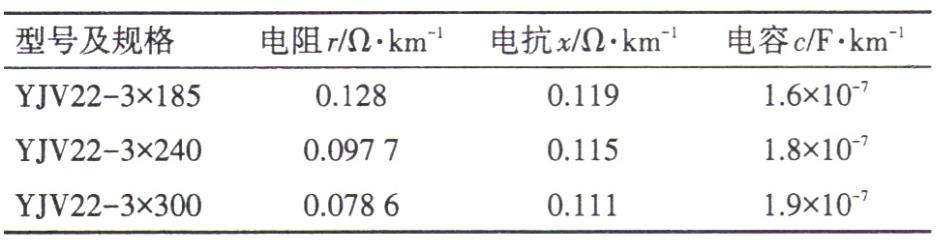
相應(yīng)的,電纜線路的潮流計算參數(shù)可由式(1)

式中:R為線路電阻,Ω;r為線路每公里電阻值,Ω/km ; l為線路長度 ,km; X為線路電抗 , Ω ; X為線路每公里電抗值 ,Ω /km; B為線路電納 ,S; f為電網(wǎng)頻率 ,Hz; c為線路每公里電容值 ,F。
城區(qū)配電網(wǎng)35kV電纜線路的始端(即電源側(cè))通常為220kV變電站的35kV側(cè)母線,末端(即負(fù)荷側(cè))通常為35kV變電站的高壓母線,正常方式下線路帶一臺變壓器運(yùn)行,見圖1 。

圖1 35kV電纜線路接線圖
由于220kV變電站的35kV側(cè)母線電壓正常運(yùn)行時主要取決于220kV変壓器高壓側(cè)電壓,受出線潮流影響很小,在計算電纜線路線損時可認(rèn)為固定不變,故將圖1所示電纜線路的潮流計算模型簡化為圖2 。圖 2中 R+jX為電纜線路阻抗支路 ,jB /2為電纜線路導(dǎo)納支路 ; U1、 U2分別表示線路始端和末端電壓 ;S
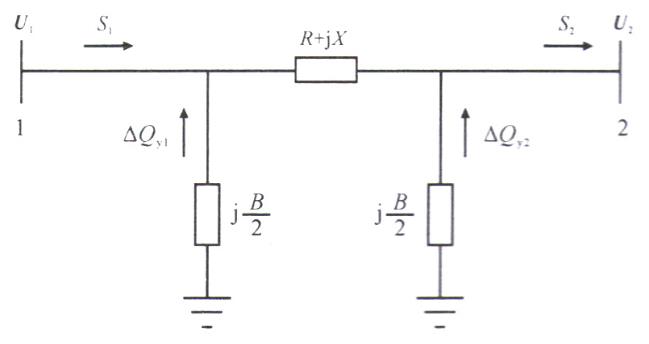
圖2 潮流計算模型
對于圖2所示已知電網(wǎng)始端電壓U1和末端功率S 2的潮流問題,可使用前推回代法進(jìn)行潮流計算 2的潮流問題,可使用前推回代法進(jìn)行潮流計算 。即首先假設(shè)電網(wǎng)各節(jié)點電壓均為額定電壓 UN∠ 0° , 由末端向始端推算功率 ,計算出始端功率 S 1 1,再根據(jù)始端電壓 U1和功率 S 1 1向末端推算潮流 ,反復(fù)多次直至滿足約束條件 。對于本文的潮流模型 , 由末端向始端推算一次 ,再由始端向末端推算一次 ,即可滿足計算精度 。
假設(shè)節(jié)點2電壓U2等于額定電壓UN∠0°,從末端向始端推算功率時,末端導(dǎo)納支路發(fā)出的無功功率為
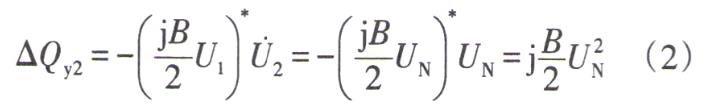
線路阻抗支路消耗的功率為
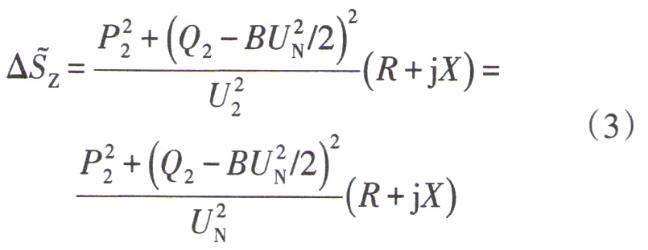
記Q’2=Q2-BUN2 /2,則式(3)可整理為 /2,則式(3)可整理為
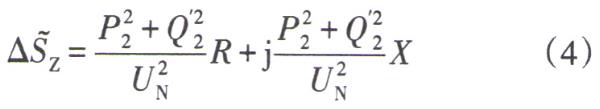
始端導(dǎo)納支路發(fā)出的無功功率為
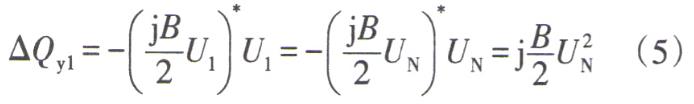
線路始端功率為
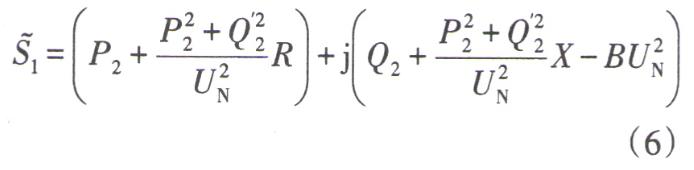
根據(jù)始端電壓,和功率向末端推算潮流,線路阻抗支路消耗的有功功率,即線路線損為

式(7)即為城區(qū)35kV電纜線路線損的計算公式 。
2 城區(qū)35kV電纜線路未端最優(yōu)無功補(bǔ)償容量
由式(7)可看出,在近似認(rèn)為電纜線路始端電壓幅值等于額定電壓的情況下,線路線損與線路參數(shù) 、末端有功功率 、無功功率有關(guān) 。對于給定的 35kV電纜線路 ,其自身參數(shù)已知 ,線路末端有功功率不可控 ,其線損只與末端無功功率有關(guān)。求取線損 P loss對末端無功功率 Q2的偏導(dǎo)數(shù)為
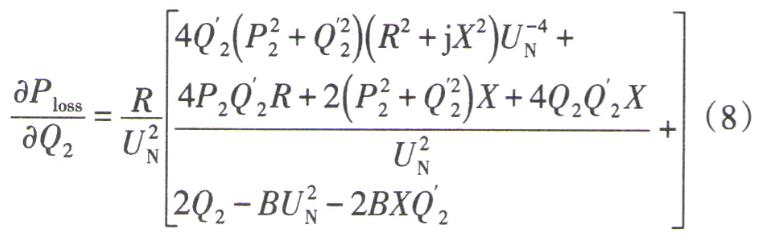
根據(jù)等網(wǎng)損微增率準(zhǔn)則,當(dāng)? P loss/? P loss/? Q2等于0時線路線損最低。令式(8)等于0,得到 Q2等于0時線路線損最低。令式(8)等于0,得到
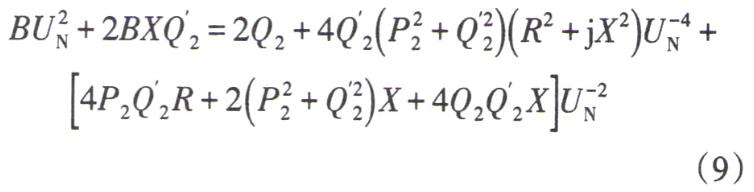
在電纜線路所帶變電站內(nèi)采取各類無功補(bǔ)償措施 ,例如在線路末端加裝電抗器、 SVC等 ,調(diào)節(jié)無功補(bǔ)償容量 ,使線路末端的無功功率 Q2滿足式 (9)時,線路線損最低 。因此式 (9)即為以線損最低為目標(biāo)的城區(qū) 35kV電纜線路末端最優(yōu)無功補(bǔ)償容量的數(shù)學(xué)模型 。值得注意的是,式 (9)是以 Q2為變量的一元三次方程 ,其 3個解中有一個實根和一對共軛虛根 ,只有實根是本文要求取的結(jié)果。
3 算例分析
首先選取天津城西電網(wǎng)最常見的YJV22-3×300型35kV電纜線路作為算例 。該型電纜的電氣參數(shù)見表 1,額定載流量為 565A,取線路長度為 4km,則潮流計算參數(shù)為

B=2×3.14×50×1.9×10-5×4=2.3864×10-4S
當(dāng)線路有功負(fù)載率為10%時 ,將線路末端有功功率 P2=3.425MW和上述線路參數(shù)代入式 (9),得到
1.54×10-3×Q23 +4.234Q22 +4.234Q22 +3.901Q2-553.84=0 +3.901Q2-553.84=0
解得Q2=0.142 Mvar,說明在線路負(fù)載率為10%的情況下,在線路末端采取各類無功補(bǔ)償措施 ,使線路末端無功功率為 0.142MW時 ,線路線損最低。選取線路有功負(fù)載率分別為 20%、 30%、… 、 80%,即線路末端有功功率分 6.85MW、 10.275MW、… 、 27.4MW共 8種運(yùn)行方式 ,按式 (9)計算線路末端最優(yōu)無功補(bǔ)償容量 ,匯總見表 2。
表2 YJV22-3×300型電纜線路末端最優(yōu)無功補(bǔ)償容量計算數(shù)值

在PSASP電力系統(tǒng)分析綜合程序中搭建如圖3聽示的簡單電網(wǎng)模型,電纜線路始端節(jié)點1為平衡節(jié)點,線路末端節(jié)點2為PQ節(jié)點,模擬電纜線路的 運(yùn)行條件。調(diào)整節(jié)點2的有功功率,仿真YJV22-3×300型電纜線路在不同負(fù)載率下使線損最低的無功補(bǔ)償容量,總結(jié)于表 3。

圖3 簡單電網(wǎng)模型
表3 YJV22-3×300型電纜線路末端最優(yōu)無功補(bǔ)償
容置仿真數(shù)值

對比表2、3可看出,根據(jù)式 (9)計算得到的線路末端最優(yōu)無功補(bǔ)償容量與仿真數(shù)值基本一致,相對誤差不超過 5%,驗證了本文所提城區(qū)35kV電纜線路末端最優(yōu)無功補(bǔ)償數(shù)學(xué)模型的正確性。其誤差主要在于式 (9)的推導(dǎo)過程中,近似認(rèn)為線路末端電壓為額定電壓,而實際上線路末端電壓與額定電壓總會有偏差 。由表 3還可看出在采取最優(yōu)無功補(bǔ)償?shù)那闆r下線路末端電壓(即35kV變電站的高壓母線電壓)始終在合格范圍內(nèi)(34~37.5kV),保證了供電質(zhì)量 。
按照同樣方法對另外幾種常見的YJV22-3×300*2型電纜線路、YJV22-3×240型電纜線路和YJV22-3×240*2型電纜線路末端最優(yōu)無功補(bǔ)償進(jìn)行仿真 ,結(jié)果匯總于表 4,線路長度均取 4km, *2表示雙回電纜線路 。雙回電纜線路由于運(yùn)行時每回之間有耦合電容存在,其每回電纜的電納參數(shù)應(yīng)乘以 2處理 。
將表3-4中各型號電纜線路末端最優(yōu)無功補(bǔ)償容量隨負(fù)載率變化的曲線匯于圖4中。由圖4可得到以下幾個結(jié)論:
l)YJV22-3x300型電纜線路負(fù)載率低于60%,YJV22-3X240型電纜線路負(fù)載率低于70%時 ,線路末端應(yīng)吸收感性無功功率以使線損最低 ;而 YJV22-3x300*2 型和 YJV22-3x240*2型電纜線路負(fù)載率達(dá)到 80%時,線路末端仍需吸收感性無功功率才能使線損最低 。換言之,城區(qū) 35kV電纜線路運(yùn)行時 ,末端消耗適當(dāng)?shù)母行詿o功功率有利于降低線損 。
2)相同長度 、相同規(guī)格的電纜,在同樣的負(fù)載率下為使線損最低 ,雙回電纜線路比單回線路需要多消耗或少補(bǔ)償感性無功功率。這是因為電纜線路阻抗支路消耗的無功功率 ? QX QX的表達(dá)式近似為
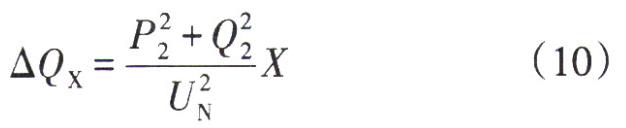
? QB充電功率的表達(dá)式近似為 QB充電功率的表達(dá)式近似為

表4 幾種常見電纜線路末端最優(yōu)無功補(bǔ)償容量仿真數(shù)值
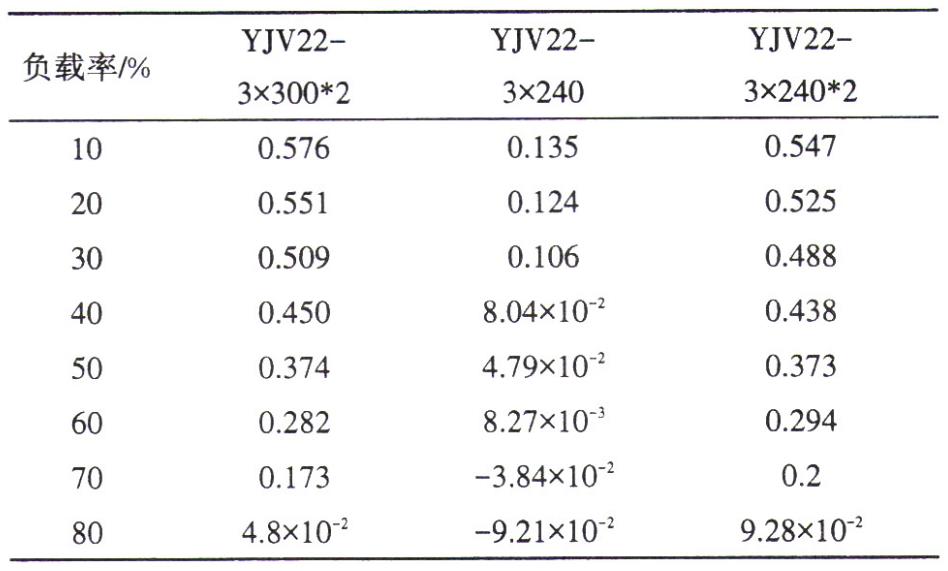
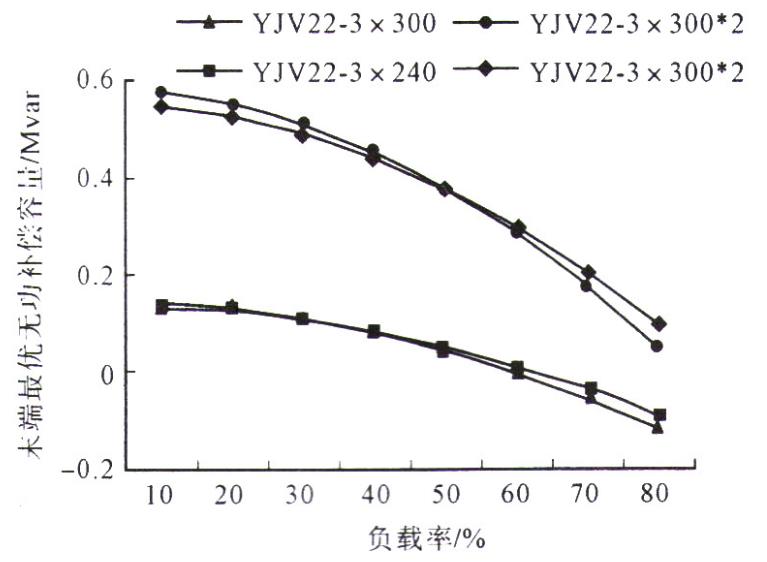
圖4 最優(yōu)無功補(bǔ)償容量曲線
潮流計算模型中相同規(guī)格 、相同長度的雙回電纜線路的阻抗是單回線路的一半,電納是單回線路的 4倍 ,因此雙回線路阻抗支路消耗的無功功率近似為單回線路的 2倍 ,而充電功率近似為單回線路的 4倍,因此為了使無功功率就地平衡 ,降低線損,雙回電纜線路比單回線路需要多消耗或少補(bǔ)償感性無功功率 。
3)城區(qū)35kV電纜線路末端最優(yōu)無功補(bǔ)償容量隨負(fù)載率變化的關(guān)系近似為二次曲線。以 YJV22-3x300*2型電纜為例,其曲線擬合函數(shù)為
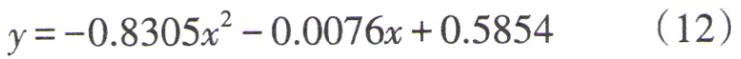
式中y表示電纜線路末端最優(yōu)無功補(bǔ)償容量 , x為以小數(shù)表示的負(fù)載率,擬合曲線對觀測值的擬合優(yōu)度 R2約等于 1。這是因為在近似認(rèn)為線路兩端電壓均是額定電壓的條件下電纜線路阻抗支路消耗的無功功率大小主要取決于線路負(fù)載和電抗值,充電功率大小主要取決于線路電納值 ,受線路負(fù)載影響很小,對于給定型號和長度的電纜線路 ,其運(yùn)行時充電功率基本不變 ,而阻抗支路消耗的無功功率與負(fù)載近似為平方關(guān)系,因此為了使電纜線
路達(dá)到線損最低的運(yùn)行狀態(tài) ,其末端最優(yōu)無功補(bǔ)償容量隨負(fù)載率變化的關(guān)系近似為二次曲線 。
4 結(jié)語
本文利用潮流計算推導(dǎo)出了城區(qū)35kV電纜線路線損的數(shù)學(xué)公式 ,建立了以線損最低為目標(biāo)的城區(qū) 35kV電纜線路末端最優(yōu)無功補(bǔ)償容量的數(shù)學(xué)模型 。通過 PSASP仿真計算驗證了該模型的正確性,給出了 4種常見型號 35kV電纜線路在不同負(fù)載率下的末端最優(yōu)無功補(bǔ)償容量數(shù)值 ,并得到以下結(jié)論:
1) 城區(qū)35kV電纜線路運(yùn)行時,特別是輕載運(yùn)行時 ,末端消耗適當(dāng)?shù)母行詿o功功率有利于降低線損 。
2) 相同長度 、相同規(guī)格的電纜 ,在同樣的負(fù)載
率下為使線損最低,雙回電纜線路比單回線路需要多消耗或少補(bǔ)償感性無功功率 。
3) 城區(qū)35kV電纜線路末端最優(yōu)無功補(bǔ)償容量隨負(fù)載率變化的關(guān)系近似為二次曲線 。
隨著供電企業(yè)日益追求精益化管理,在保證良好的電能質(zhì)量的前提下盡可能降低網(wǎng)損 ,減少供電企業(yè)生產(chǎn)成本的重要性日趨增大 。本文給出的城區(qū)35 kV電纜線路末端最優(yōu)無功補(bǔ)償容量的數(shù)學(xué)模型及4種常見型號35kV電纜線路在不同負(fù)載率下的末端最優(yōu)無功補(bǔ)償容量數(shù)值對于城區(qū)供電企業(yè)降損具有指導(dǎo)意義。
|
